Skip to main content Link Search Menu Expand Document (external link)

Core Concepts

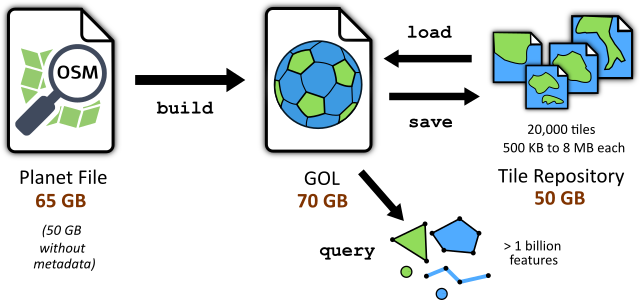
The heart of GeoDesk is a spatial database engine, which stores OpenStreetMap data in a Geographic Object Library (GOL). You can create GOLs from .osm.pbf files using the gol command-line tool, or download data tiles from a repository.

Coordinate System

OpenStreetMap uses degrees longitude and latitude to store coordinates. GeoDesk represents features using a spherical Mercator projection. This type of projection has several advantages: the shapes and angles of features are preserved locally, north is always up, and geometric operations are simplified. The maps on OpenStreetMap are displayed in Mercator projection.

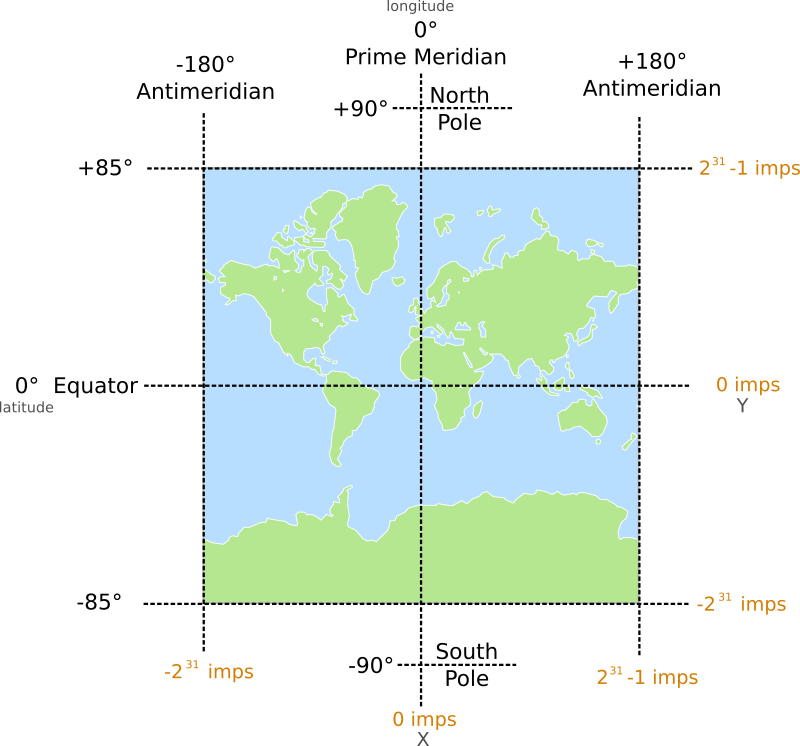
GOLs store coordinates as 32-bit integers, using an artificial unit called imp (integer, Mercator-projected). This allows for a coordinate resolution of roughly 1 centimeter.

  • The Earth (excluding polar areas) is represented as a square, 232 imps high and wide
  • Coordinates use the full 32-bit integer range; the minimum and maximum X coordinates represent the Antimeridian (+/- 180 degrees longitude)
  • Coordinates increase from west to east, and from south to north (Unlike screen coordinates, Y coordinates decrease moving “downward”)
  • Positive X coordinates are located in the eastern hemisphere, negative in the western
  • Positive Y coordinates are located north of the Equator, negative in the south

Problems with Mercator (and how to solve them)

Any method that attempts to represent the Earth’s surface as a flat plane involves compromises. The Mercator projection is no exception — it has two principal drawbacks.

The first one you have already noticed: Mercator cannot represent polar areas. For OpenStreetMap data, this is hardly an issue. While OSM can store coordinates of any feature on Earth, it contains little data at latitudes above 85 degrees — after all, besides ice shelves and rocks, there just isn’t much to be mapped (If you’re location scouting for the sequel to March of the Penguins, sorry, you’re out of luck).

The second problem requires closer attention. Have a look at this Mercator-projected world map:

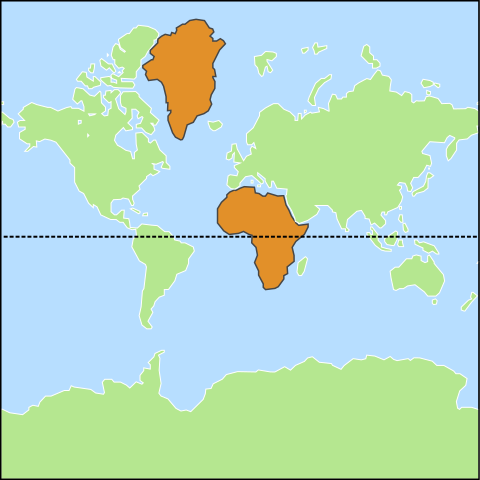
Greenland and Africa appear to be roughly the same size — in reality, Africa is 14 times larger than Greenland.

Mercator projection distorts areas, especially those far from the Equator, which can make it more difficult to accurately measure features. As long as a feature is relatively small, this distortion is negligible, and the measurement functions provided by GeoDesk automatically apply the proper scale factor based on the object’s latitude. Unfortunately, this simplified approach doesn’t work well for larger features, especially if they stretch north-south and are distant from the Equator. If you want to measure the landmass of Canada with a reasonable degree of accuracy, you will need to transform its geometry to an equal-area projection (such as Canada Albers). The Proj4J Java library can help you with this task.

In general, you should be aware of the limitations of using planar geometry for geospatial calculations. Using the Euclidean distance formula to calculate the length of road segments is perfectly fine, but if you calculate the air distance from London to Los Angeles this way, you will get wildly inaccurate results.

Bottom line: As for all software solutions, it pays to know when a fast and simple method is sufficient, and which situations require a more sophisticated approach.